Clustering in R (Analisi dei gruppi).

Prima di spiegare come effettuare un clustering in R, diamo una definizione. Il clustering (o analisi dei gruppi) è un metodo di data analisi unsupervised usato in diversi campi (pattern recognition, scienze sociali, marketing, farmaceutico, …). Per clustering si intende il processo di raggruppamento di un insieme di oggetti fisici o astratti in classi di oggetti simili (Han 2001). Il cluster, quindi, è una collezione di oggetti simili tra loro e che sono dissimili rispetto ad oggetti di altri cluster.
Esistono diverse tecniche di clustering e si basano su misure relative alla somiglianza tra elementi. In molti approcci questa similarità (o dissimilarità) è concepita in termini di distanza in spazi multidimensionali.
Vediamo adesso come effettuare un Clustering in R.
Il primo passo è quello di preparare i dati rimuovendo o stimando i dati mancanti.

# Prepare Data
mydata <- na.omit(mydata) # Eliminare i dati mancanti
mydata <- scale(mydata) # Standardizzare le variabili


Clustering gerarchico in R

Nel package stats abbiamo la funzione hclust per il clustering gerarchico. La funzione hclust riceve una matrice distanza come argomento.
Utilizziamo come dataset (anche se molto piccolo) mtcars Motor Trend Car Road Tests.

d<-dist(mtcars, method = "euclidean")
#i metodi possibili per la distanza sono "aitchison", "euclidean", "maximum", "manhattan", "canberra", "binary" or "minkowski"
h<-hclust(d)
h

Call:
hclust(d = d)

Cluster method : complete
Distance : euclidean
Number of objects: 32

#graficamente
plot(h)


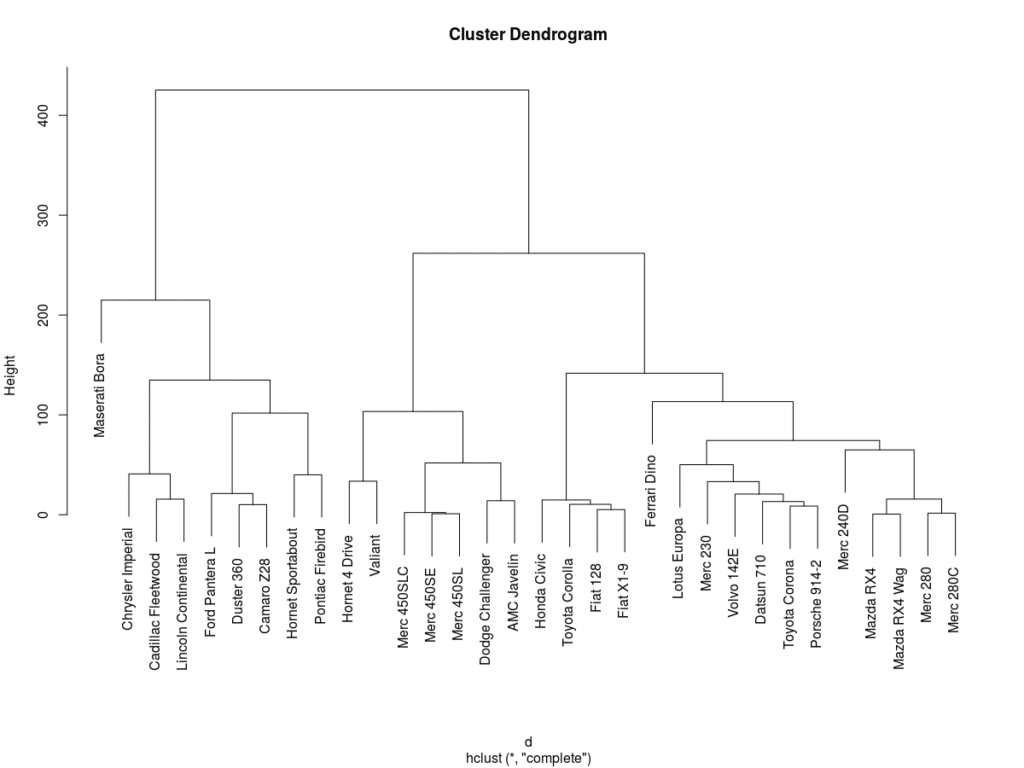
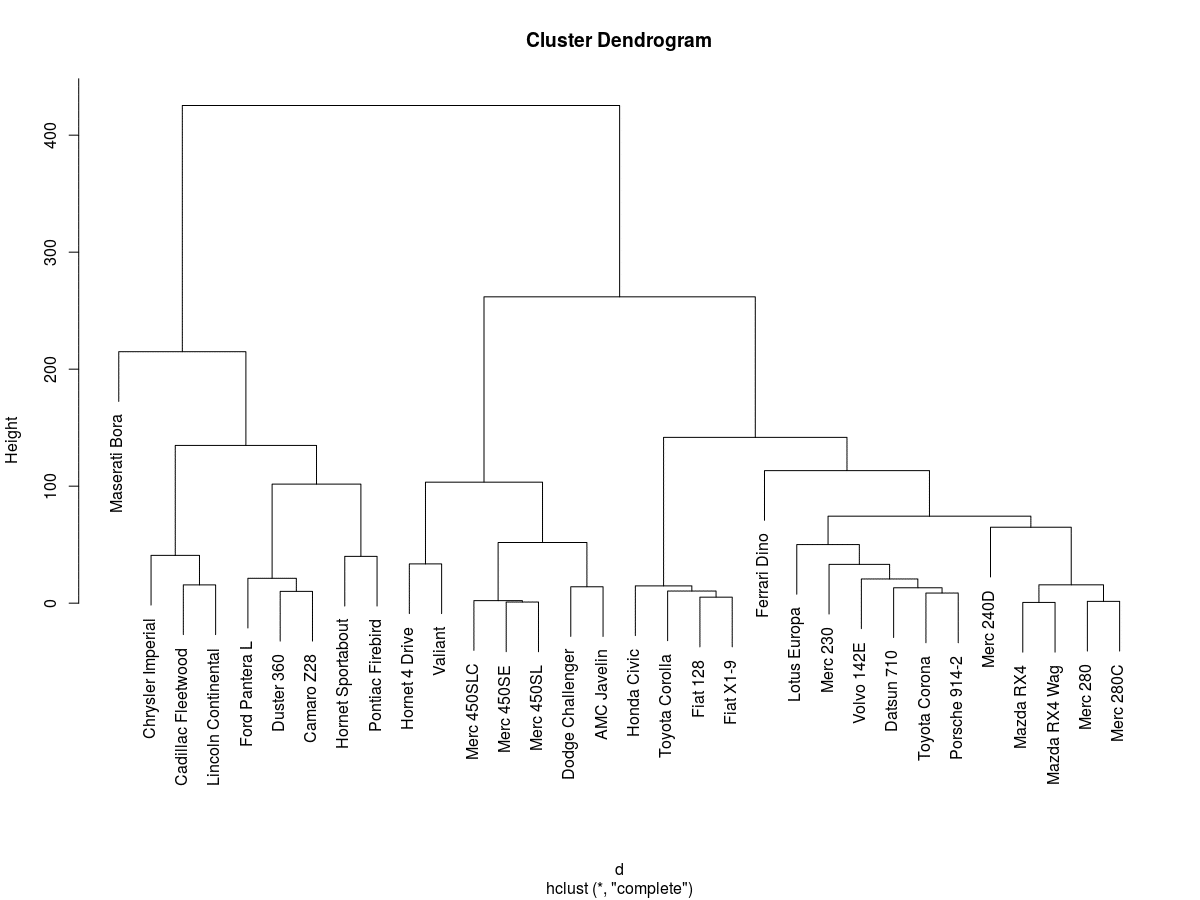
Il risultato finale è una serie di partizioni rappresentate graficamente attraverso un “dendrogramma” o “diagramma ad albero”. Ogni ramo del diagramma corrisponde ad un grappolo (gruppo o cluster), la linea di congiunzione di due o più rami indica la distanza al quale i grappoli si fondono.

K-means clustering in R

Nel package stats abbiamo la funzione kmeans per il K-means clustering in R, specificando il dataset e il numero di cluster.

k <- kmeans(mtcars, 3)
k
K-means clustering with 3 clusters of sizes 9, 16, 7

Cluster means:
mpg cyl disp hp drat wt qsec vs am gear carb
1 14.64444 8.000000 388.2222 232.1111 3.343333 4.161556 16.40444 0.0000000 0.2222222 3.444444 4.000000
2 24.50000 4.625000 122.2937 96.8750 4.002500 2.518000 18.54312 0.7500000 0.6875000 4.125000 2.437500
3 17.01429 7.428571 276.0571 150.7143 2.994286 3.601429 18.11857 0.2857143 0.0000000 3.000000 2.142857

Clustering vector:
Mazda RX4 Mazda RX4 Wag Datsun 710 Hornet 4 Drive Hornet Sportabout
2 2 2 3 1
Valiant Duster 360 Merc 240D Merc 230 Merc 280
3 1 2 2 2
Merc 280C Merc 450SE Merc 450SL Merc 450SLC Cadillac Fleetwood
2 3 3 3 1
Lincoln Continental Chrysler Imperial Fiat 128 Honda Civic Toyota Corolla
1 1 2 2 2
Toyota Corona Dodge Challenger AMC Javelin Camaro Z28 Pontiac Firebird
2 3 3 1 1
Fiat X1-9 Porsche 914-2 Lotus Europa Ford Pantera L Ferrari Dino
2 2 2 1 2
Maserati Bora Volvo 142E 1 2
Within cluster sum of squares by cluster:
[1] 46659.32 32838.00 11846.09
(between_SS / total_SS = 85.3 %)

Available components:

[1] "cluster" "centers" "totss" "withinss" "tot.withinss" "betweenss" "size"
[8] "iter" "ifault"


Rispetto al cluster gerarchico abbiamo maggiori informazioni.

Determinare il numero di cluster

Il package NbClust offre un conveniente metodo per l’esplorazione dei dati prima di eseguire il clustering in R.

library(NbClust)
NbClust(iris[, -5], method = 'complete', index = 'all')$Best.nc[1,]
*** : The Hubert index is a graphical method of determining the number of clusters.
In the plot of Hubert index, we seek a significant knee that corresponds to a
significant increase of the value of the measure i.e the significant peak in Hubert
index second differences plot.

*** : The D index is a graphical method of determining the number of clusters.
In the plot of D index, we seek a significant knee (the significant peak in Dindex
second differences plot) that corresponds to a significant increase of the value of
the measure.

*******************************************************************
Among all indices:
2 proposed 2 as the best number of clusters
13 proposed 3 as the best number of clusters
5 proposed 4 as the best number of clusters
1 proposed 6 as the best number of clusters
2 proposed 15 as the best number of clusters
***** Conclusion *****
* According to the majority rule, the best number of clusters is 3
*******************************************************************
KL CH Hartigan CCC Scott Marriot TrCovW TraceW Friedman Rubin
4 4 3 3 3 3 3 3 4 6
Cindex DB Silhouette Duda PseudoT2 Beale Ratkowsky Ball PtBiserial Frey
3 3 2 4 4 3 3 3 3 1
McClain Dunn Hubert SDindex Dindex SDbw
2 15 0 3 0 15


Attraverso NbClust è possible avere una stima (attraverso alcuni indici) sul numero di cluster da scegliere.

Guarda tutti i tutorial di Statistica Avanzata oppure torna su R tutorial.